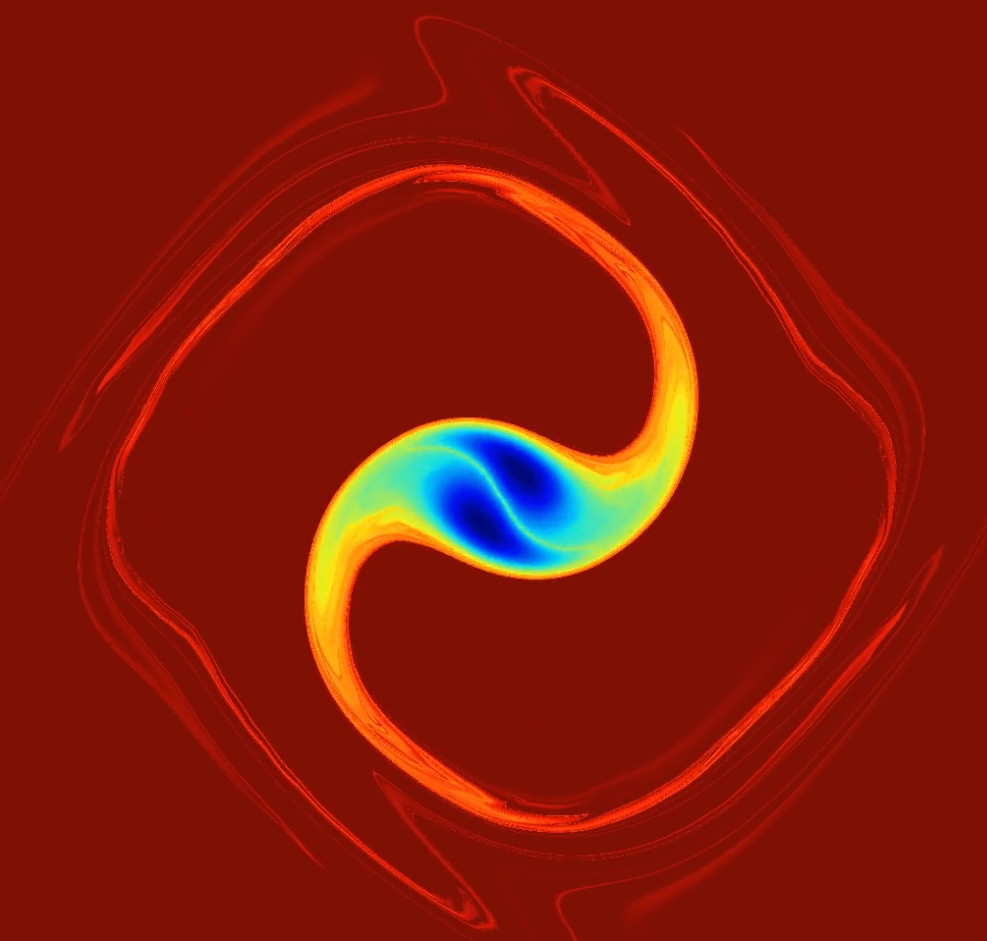
In this project, we introduce the characteristic mapping method to address the complexity of high- dimensional kinetic equations, such as those involving ion-electron interactions in plasma fusion, by integrating mathematical modeling with high-performance computing. This semi-Lagrangian method achieves exponential resolution in linear time, revealing fine-scale details of the solutions and providing insights into the filamentation structure of plasmas. By employing reduced-order models, we significantly lower the numerical complexity of the computations. Our approach, which combines dimensionality reduction of sub-maps with refinement through map compositions via the solution operator, is innovative and paves the way for efficient evaluation of high-dimensional distribution functions across extended time intervals and multi-scale spatial domains. This project is designed to test the potential to enhance existing semi-Lagrangian techniques and advance our understanding of intricate local thermodynamic non-equilibrium phenomena in plasmas, with applications in magnetically confined fusion.

Team:

LAGA, UMR 7030, Université Sorbonne Paris Nord
Olivier Lafitte (PI)
lafitte(at)math.univ-paris13.fr

CEA - IRFM, Cadarache
Kevin Obrejan
kevin.obrejan(at)cea.fr,

I2M, UMR 7373, Aix-Marseille Université
Kai Schneider
kai.schneider(at)univ-amu.fr

Department of Mathematics and Statistics, McGill University, Montreal
Jean-Christophe Nave —

Visit the old Adaptive-CMM project →