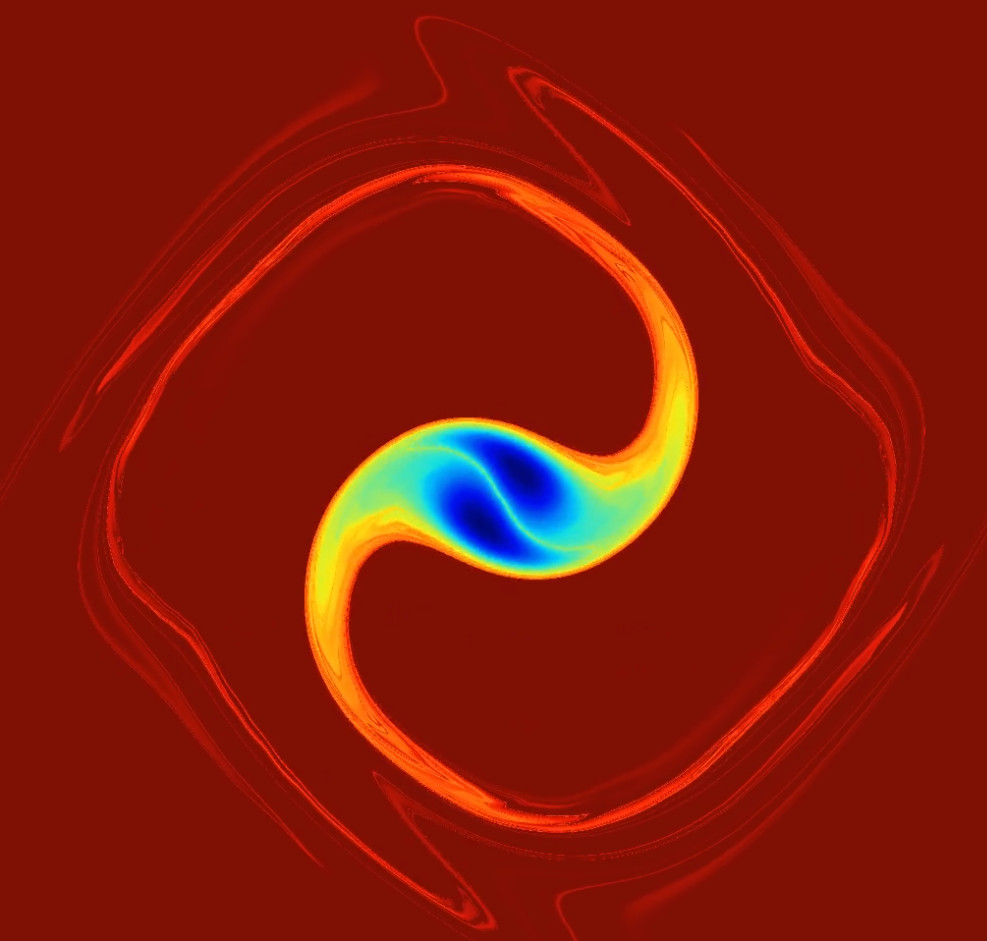
Adaptive Characteristic Mapping Method for the Euler Equations (CM2E)

About the adaptive-CMM project

Even though computational resources grow rapidly, the extremely fine scales in fluid and plasma turbulence remain beyond reach using existing numerical methods. A combination of computational power and ingenious physical insights is usually needed to go beyond the brute force limit. We propose here to develop a novel numerical method, a fully Adaptive Characteristic Mapping Method (ACMM) for evolving the flow map, which yields exponential resolution in linear time. The first results for the 2D incompressible Euler equations show the extremely high-resolution capabilities of the scheme. The project consists of 2 parts. Part one is focused on the development of ACMM for 2D systems, including its adaptive version using multiresolution techniques and subsequently, its application to 2D Euler flows, passive scalar mixing and magnetic reconnection problems. In the second part, we will extend the method to 3D and investigate the formation of singularities and turbulent dissipation.

Consortium:

I2M, UMR 7373, Aix-Marseille Université
Kai Schneider (PI and coordinator)

LMFA, UMR 5509, Ecole Centrale de Lyon, Université de Lyon
Wouter Bos (coordinator)

CRM, UMI 3457, Montreal
Olivier Lafitte (coordinator)

McGill University, Montreal
Jean-Christophe Nave (coordinator)

Master and PhD thesis:

• B. Yadav, Characteristic Mapping Method for Incompressible Euler Equations. Master thesis. McGill University, 2015. [pdf]

• N. Saber, Two-dimensional Characteristic Mapping Method with inertial particles on GPU using CUDA, Master thesis, I2M-AMU, July 2021. [pdf]

• J. Bergmann, Investigation of mixing and particle transport in 2D incompressible Euler flows using the characteristic mapping method, Master thesis, I2M-AMU, April 2022. [pdf]

• X.-Y. Yin, Characteristic mapping framework with applications to density transport and fluid dynamics, PhD thesis, McGill, 2022 [pdf]

• M. Bolduc, A Fourier spectral method with high resolution for advection problems, Master thesis, McGill University, April 2023

• M. A. Sahakian, A Characteristic mapping method for two-dimensional magnetohydrodynamic equations, Master thesis, I2M-AMU, September 2023

Publications

• A Characteristic Mapping Method for Vlasov-Poisson with Extreme Resolution Properties
  P. Krah, X.-Y. Yin, J. Bergmann, J.-C. Nave, K. Schneider
  Communications in Computational Physics 35 (4), 905–937, 2024. arXiv:2311.09379
  [PDF]

• Singularity formation of vortex sheets in 2D Euler equations using the characteristic mapping method
  J. Bergmann, T. Oujia, X.-Y. Yin, J.-C. Nave and K. Schneider
  Preprint, 01/2023

• A Characteristic Mapping Method for the three-dimensional incompressible Euler equations
  X.-Y. Yin, K. Schneider and J.-C. Nave.
  J. Comput. Phys., 477, 111876, 2023. arXiv:2107.03504
  [PDF]

• A Characteristic Mapping Method for the two-dimensional incompressible Euler equations
  X.-Y. Yin, O. Mercier, B. Yadav, K. Schneider and J.-C. Nave
  J. Comput. Phys., 424, 109781, 2021. arXiv:1910.10841
  [PDF]

• Computing differential operators of the particle velocity in moving particle clouds using tessellations
  T. Oujia, K. Matsuda and K. Schneider
  Preprint, 12/2022. arXiv:2212.03580
  [PDF]

• Clustering of inertial particles in turbulent flow through a porous unit cell
  S. V. Apte, T. Oujia, K. Matsuda, B. Kadoch, X. He and K. Schneider
  J. Fluid Mech., 937, A9, 2022. arXiv:2108.10366
  [PDF]

• Divergence and convergence of inertial particles in high Reynolds number turbulence
  T. Oujia, K. Matsuda and K. Schneider
  J. Fluid Mech., 905, A14, 2020. arXiv:2005.00525
  [PDF]

List of conference proceedings and presentations

• JC Nave, Méthodes à résolution arbitraire :du transport linéaire à l’équation d’Euler, Univ. Paris Dauphine, March 2021

• JC Nave, Numerical Solution to the Incompressible Euler’s Equations with Arbitrary Resolution, 2021 SIAM Conference on Computational Science and Engineering (CSE21), July 2021

• X.-Y. Yin, K. Schneider and J.-C. Nave. Numerical solution of the three-dimensional incompressible Euler equations using the Characteristic Mapping Method, 74th Annual Conference, Division of Fluid Dynamics, American Physical Society, Phoenix (USA), 21-23.11.2021. Bull. Amer. Phys. Soc., 66(17), 2021.

• JC Nave, Fourier spectral method for transport and fluid problems with arbitrary fine scales, CAIMS Annual meeting, June 2022

• T. Oujia, K. Matsuda, K. Schneider. Extreme divergence and rotation values of the inertial particle velocity in high Reynolds number turbulence using Delaunay tesselation, 12th International Symposium on Turbulence and Shear Flow Phenomena (TSFP12), Jul 2022, Osaka, Japan.

• K. Matsuda, T. Oujia and K. Schneider. Clustering formation of inertial particles in homogeneous isotropic turbulence, 11th International Conference on Multiphase Flow, Apr 2023, Kobe, Japan, accepted.

• T. Oujia, J. West, K. Matsuda, K. Schneider, S. Jain and K. Maeda. Divergence and rotation of inertial particles in a four-way coupled channel flow 11th International Conference on Multiphase Flow, Apr 2023, Kobe, Japan, accepted.

• J. Bergmann, T. Oujia, X.-Y. Yin, J.-C. Nave and K. Schneider. High resolution vortex layer computations in 2D Euler flows using a characteristic mapping method, 75th Annual Conference, Division of Fluid Dynamics, American Physical Society, Indianapolis (USA), 20-22.11.2022.

• Xi-Yuan Yin, Characteristic Mapping method and applications to the singularity problem in the 3D Euler equations, GDR turbulence, Lille 2-4/11/2022.

Movies

• Vortex merge simulation of incompressible Euler
• Two stream instability simulation of Vlasov-Poisson

Team:

Former team members are marked with (*)

• Thibault Oujia, PhD student, I2M Marseille
• Julius Bergmann (*), Master student, I2M Marseille (TU Berlin)
• Nicolas Saber (*), Master student, I2M Marseille
• Miriam Goldeck (*) Internship, I2M Marseille
• Philipp Krah, Postdoc, I2M Marseille
• Benjamin Kadoch, Faculty, IUSTI Marseille
• Kai Schneider, Faculty, I2M Marseille (PI and coordinator Marseille)
• Marc Antonio Sahakian, Master Student, I2M Marseille
• Xi-Yuan (Bruce) Yin, Postdoc, LMFA Lyon
• Tong Wu, PhD student, LMFA Lyon

• Wouter Bos, Faculty, LMFA Lyon (coordinator Lyon)

• Manuel Bolduc, Master student, McGill Montreal
• William Holman-Besinger, Master student, McGill Montreal
• Jean-Christophe Nave, Faculty, McGill (coordinator Montreal McGill)
• Olivier Lafitte, Faculty, CRM (coordinator Montreal CRM)